Pytorch - 基于卷积神经网络的CIFAR-10数据集分类模型训练与检测

小白劝退预告

• 仅简单介绍思路，没有用作教程的打算，如果读者没有机器学习基础、计算机视觉基础或Pytorch基础 —— 会很不友好的(

CIFAR-10数据集介绍

CIFAR-10数据集的内容

• CIFAR10数据集共有60000个样本，每个样本都是一张32*32像素的RGB图像(彩色图像)，每个RGB图像又必定分为3个通道(R通道、G通道、B通道)。这60000个样本被分成了50000个训练样本和10000个测试样本
• CIFAR10数据集是用来监督学习训练的，那么每个样本就一定都配备了一个标签值(用来区分这个样本是什么)，不同类别的物体用不同的标签值，CIFAR10中有10类物体，标签值分别按照0~9来区分,他们分别是飞机(airplane)、汽车(automobile)、鸟(bird)、猫(cat)、鹿(deer)、狗(dog)、青蛙(frog)、马(horse)、船(ship)和卡车(truck)
• CIFAR10数据集的内容，如图所示

总的来说，CIFAR-10数据集有以下优势：

• 图片像素小，处理快，便于入门
• 数据量大，且下载便利
• 已提前做好数据标注，提供专用API，使用便捷
• 彩色图片，RGB三通道，考验进阶思维

Pytorch实现神经网络

Pytorch 加载 CIFAR-10 数据集

首先，利用 torchvision.dataset 对象内置的 API 获取数据集; 并利用变换函数(transform 参数)对读取的图片实现 tensor 化和正则化。torchvision.transforms 对象内置了一些函数能帮我们实现这一要求，该对象内置了 Compose函数，可以便捷地为我们打包一系列的数据预处理变换 —— 比如 tensor 化和正则化
其次，利用 torch.utils.data.DataLoader 对象为 torchvision.dataset 对象套上一个加载器，可以便捷地给我们返还数据和标签

from torchvision import datasets, transforms
from torch.utils.data import DataLoader

transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)),
])

trainset = datasets.CIFAR10(
    'data/',              # 指定下载路径
    train=True,           # 训练集应标为 train=True
    download=True,        # 指定是否下载数据
    transform=transform   # 指定图片变换函数
)
testset = datasets.CIFAR10(
    'data/',
    train=False,
    download=True, 
    transform=transform
)

trainloader = DataLoader(
    trainset,             # 指定需要迭代的数据集
    shuffle=True,         # 加载时是否打乱数据
    batch_size=4,         # 一次返回的数据规模
    num_workers=2         # 加载数据时使用的进程数
)
testloader  = DataLoader(
    testset, 
    shuffle=False,
    batch_size=4,
    num_workers=2
)

Pytorch 实现卷积神经网路

torch.nn.Module 对象内置了前向传播和参数设置等一系列的 API，我们自己定义一个继承自 torch.nn.Module 对象的类便于我们的后续操作
下列部分都是基本的 Pytorch 语法，不过多做解释，在这里我打算推演一遍单张图片的这个 tensor 的尺寸该如何计算：

1. 图片是彩色、采用 rgb 编码的 32 * 32 像素的图片。rgb 编码意味着这张图由 r、g、b 三张特征图构成，每张特征图的尺寸都是 32 * 32，故最早的输入尺寸是 (3, 32, 32)
2. 第一次卷积，从 3 张特征图生成为 6 张特征图; 同时卷积会让图片的长宽损失一定的大小，对于本次训练，长宽各损失了 2 * (5 - 1) / 2 = 4 个像素点，故经过第一层卷积后，图片数据尺寸变为 (6, 28, 28)
3. 第一次池化，池化是指将图片长款压缩，对于本次训练，长宽均压缩为原来的 1/2，故此时图片数据尺寸变为 (6, 14, 14)
4. 第二次卷积，原理与第一次卷积相同，最终得到数据尺寸为 (16, 10, 10)
5. 第二次池化，原理与第一次池化相同，故此时图片数据尺寸变为 (16, 5, 5)
6. 将多次卷积、池化后的图片数据一维化，强制变为一维张量，即此时数据尺寸为 (-1, 16 * 5 * 5)
7. 将上述得到的含有 400 元素的张量多次输入到线性回归层中，最终得到 10 个数值，分别代表了 10 个分类的正确概率
8. 上述的所有操作都会经过 relu() 激活函数用以非线性化，relu() 函数不会改变数据尺寸，故不考虑

from torch import nn
import torch.nn.functional as F

class Net(nn.Module):                               # 定义一个类，用作我们的神经网络，继承自 torch.nn.Module
    def __init__(self):
        super(Net, self).__init__()
        self.c1 = nn.Conv2d(3, 6,  (5, 5))          # 定义一个卷积核，从 3 张特征图生成出 6 张特征图， 核的大小为 5 x 5
        self.c2 = nn.Conv2d(6, 16, (5, 5))          # 定义一个卷积核，从 6 张特征图生成出 16 张特征图，核的大小为 5 x 5
        self.f1 = nn.Linear(16 * 5 * 5, 120)        # 定义一层神经网络，400 个数据输入，120 个数据输出
        self.f2 = nn.Linear(120, 84)                # 定义一层神经网络，120 个数据输入，840 个数据输出
        self.f3 = nn.Linear(84, 10)                 # 定义一层神经网络，84 个数据输入，10 个数据输出
        return
        
    def forward(self, x):
        x = F.max_pool2d(F.relu(self.c1(x)), 2)     # 对图片做卷积操作，再池化为原来的 1/2，此时图片数据从 3 * 32 * 32 变成 6 * 14 * 14
        x = F.max_pool2d(F.relu(self.c2(x)), 2)     # 对图片做卷积操作，再池化为原来的 1/2，此时图片数据从 6 * 14 * 14 变成 16 * 5 * 5
        x = x.view(-1, 16 * 5 * 5)                  # 将两次卷积后的 16 张 5 x 5 的特征图拉伸为 400 个元素的张量
        x = F.relu(self.f1(x))                      # 将 400 个元素输入到神经层，获得 120 个输出
        x = F.relu(self.f2(x))                      # 将 120 个元素输入到神经层，获得 84 个输出
        x = self.f3(x)                              # 将 84 个元素输入到神经层，获得 10 个输出
        return x

定义超参数

超参数就是全局变量，我们需要定义以下几个超参数：

1. model: 要训练的模型，实例化上文我们定义的类即可
2. epoches: 训练批数，每批训练 14000 次
3. learning_rate: 学习率，控制着模型训练速率的常数
4. criterion: 损失函数，本质为 torch.nn 对象，对于多分类的模型，我们采用交叉熵函数(即 CrossEntropyLoss )
5. optimizer: 模型优化器，本质为 torch.optim 对象，在本次训练中，我们选择 SGD(Stochastic Gradient Descent，即随机梯度下降优化) 作为我们模型的优化方法

from torch import nn, optim

model = Net()                                                 # 实例化 Net() 对象
epoches = 1                                                   # 指定训练批次
learning_rate = 1e-2                                          # 确定学习率
criterion = nn.CrossEntropyLoss()                             # 确定损失函数
optimizer = optim.SGD(model.parameters(), lr=learning_rate)   # 确定优化器

实现检测

这个函数用于计算我们的模型正确率如何
首先，我们定义了两个变量，分别为 correct —— 存放识别正确的个数、total —— 存放所有的数据个数
每次迭代获取数据时，用模型做预测，将预测结果与真实结果相等的结果存放进 predicts 里
依次对 correct 和 total 更新，最终返回二者比值便是模型正确率

import torch

def test():
    correct = 0.0                                           # correct 存放正确个数
    total   = 0.0                                           # total 存放总个数
    for data in testloader:
        inputs, labels = data                               # 获取数据
        outputs = model(inputs)                             # 获得预测结果
        
        predicts = (torch.max(outputs, 1)[1] == labels)     # 获取预测结果与真实结果的相等情况
        correct += predicts.sum()                           # 更新 correct
        total   += labels.size(0)                           # 更新 total
    
    acc = correct / total                                   # 计算获得正确率
    return acc                                              # 返回正确率

Pytorch 实现训练过程

我们将模型的训练过程整合成为一个函数，这个函数接受一个输入: epoches，即训练的批数；它将不断优化模型的参数，不断降低损失函数的值
我们拆分这个训练过程，它主要由这几步构成：

1. 每次训练，将训练的图片数据存进 inputs 里，将训练数据对应的标签存进 labels 里
2. 通过模型计算得到结果，存进 outputs 里，并通过损失函数得到损失值 loss
3. 先清空模型的参数梯度设置，调用 loss 的反向传播重新计算梯度，并依据梯度对模型参数赋值
4. 每 1000 次训练，计算这轮计算的时间、损失值、正确率，用作训练时的日志输出，同时将关键数据存入容器中，为后续的可视化做铺垫
5. 函数最终返回三个容器，分别存放了特殊训练次数对应的损失值和准确率

from time import perf_counter

def train(epoches=1):
    step_list = []                                      # 存放训练次数的容器
    loss_list = []                                      # 存放训练次数对应的损失值的容器
    acc_list  = []                                      # 存放训练次数对应的准确度的容器
    for epoch in range(1, epoches + 1, 1):
        start = perf_counter()                          # 设置一个计时起点
        for step, data in enumerate(trainloader, 0):    # 对数据集做迭代
            inputs, labels = data                       # 获得图片数据和标签数据
            outputs = model(inputs)                     # 获得当前模型的预测值
            
            loss = criterion(outputs, labels)           # 计算损失
            optimizer.zero_grad()                       # 重置模型梯度
            loss.backward()                             # 梯度反向传播
            optimizer.step()                            # 模型重新设置参数
            
            if step % 1000 == 0 and step != 0:
                step = (epoch - 1) * 12000 + step       # 计算步骤
                loss = loss.item()                      # 计算损失
                acc  = 100 * test()                     # 计算准确度
                time = perf_counter() - start           # 计算时间
                start = perf_counter()                  # 重新设置计时开始点
                
                step_list.append(step)                  # 容器添加
                loss_list.append(loss)                  # 容器添加
                acc_list.append(acc)                    # 容器添加
                
                print("[Epoch:%5d Step:%5d Loss:%5.2f Acc:%5.2f%% Time:%5.2fs]"%(epoch, step, loss, acc, time)) # 日志输出
        
    print("Finished training!")                         
    return step_list, loss_list, acc_list               # 返回值

最终 && 可视化操作

我们用 time.perf_counter() 函数来对整个训练过程计时
train() 函数最终返回三个容器，里面存放了训练过程的关键数据，我们可以通过 matplotlib.pyplot 来可视化我们的数据
我们先把这三个容器分别存入 Step、Loss、Acc 中
利用 matplotlib.pyplot 和上述三个容器，我们可视化我们的训练过程
plt.figure() 用来分隔画布，plt.show() 最终展示即可

from time import perf_counter
import matplotlib.pylot as plt

start = perf_counter()                      # 获取开始时间
Step, Loss, Acc = train(epoches)            # 获得关键训练中间数据
time = perf_counter() - start               # 计算最终训练时间
print("[Total time:%5.2fs]"%(time))

plt.figure(1)                               # 设置第 1 个画布
plt.plot(Step, Loss, 'b-')                  # 渲染第 1 个画布
plt.figure(2)                               # 设置第 2 个画布
plt.plot(Step, Acc, 'r-')                   # 渲染第 2 个画布
plt.show()                                  # 展示画布

完整代码展示

下面是整合了上文内容的完整代码

import torch
import torchvision
from torchvision import datasets, transforms
import torch.nn.functional as F
from torch import nn, optim
from torch.utils.data import DataLoader
from time import perf_counter
import matplotlib.pyplot as plt

transform_train = transforms.Compose([
    transforms.Resize(40),
    transforms.RandomResizedCrop(32, scale=(0.64, 1.0), ratio=(1.0, 1.0)),
    transforms.RandomHorizontalFlip(),
    transforms.ToTensor(),
    transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)),
])

transform_test = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)),
])

trainset = datasets.CIFAR10(
    'data/',                    # 指定下载路径
    train=True,                 # 训练集应标为 train=True
    download=True,              # 指定是否下载数据
    transform=transform_train   # 指定图片变换函数
)

testset = datasets.CIFAR10(
    'data/',
    train=False,
    download=True, 
    transform=transform_test
)

trainloader = DataLoader(
    trainset,             # 指定需要迭代的数据集
    shuffle=True,         # 加载时是否打乱数据
    batch_size=1024,      # 一次返回的数据规模
    num_workers=2         # 加载数据时使用的进程数
)

testloader  = DataLoader(
    testset, 
    shuffle=False,
    batch_size=1024,
    num_workers=2
)

def vgg_block(in_channels, out_channels):
    return nn.Sequential(
        nn.Conv2d(in_channels, out_channels, kernel_size=3, stride=1, padding=1),
        nn.BatchNorm2d(out_channels), nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=3, stride=1, padding=1),
        nn.BatchNorm2d(out_channels), nn.ReLU(),
        nn.MaxPool2d(kernel_size=2, stride=2),
    )

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.vgg = nn.Sequential(
            vgg_block(3, 16),                                 # [1, 16, 16, 16]
            vgg_block(16, 32),                                # [1, 32, 8, 8]
            vgg_block(32, 64),                                # [1, 64, 4, 4]
            nn.Flatten(),
        )
        self.linear = nn.Sequential(
            nn.Linear(64 * 4 * 4, 128),
            nn.Dropout(0.5), nn.ReLU(),
            nn.Linear(128, 84),
            nn.Dropout(0.5), nn.ReLU(),
            nn.Linear(84, 10),
            nn.Softmax(dim=1),
        )
        return
        
    def forward(self, x):
        x = self.vgg(x)
        x = self.linear(x)
        return x

model = torchvision.models.resnet18(weights=None)         
model.fc = nn.Linear(512, 10)
model = model.cuda()                                          # 实例化 Net() 对象
epoches = 50                                                  # 指定训练批次
learning_rate = 1e-3                                          # 确定学习率
criterion = nn.CrossEntropyLoss()                             # 确定损失函数
optimizer = optim.Adam(model.parameters(), lr=learning_rate)  # 确定优化器

def test():
    correct = 0.0                                           # correct 存放正确个数
    total   = 0.0                                           # total 存放总个数
    for data in testloader:
        inputs, labels = data                               # 获取数据
        inputs = inputs.cuda()
        labels = labels.cuda()
        outputs = model(inputs)                             # 获得预测结果
        
        predicts = (torch.max(outputs, 1)[1] == labels)     # 获取预测结果与真实结果的相等情况
        correct += predicts.cpu().sum()                     # 更新 correct
        total   += labels.cpu().size(0)                     # 更新 total
    
    acc = correct / total                                   # 计算获得正确率
    return acc  

def train(epoches=1):
    step_list = []                                      # 存放训练次数的容器
    loss_list = []                                      # 存放训练次数对应的损失值的容器
    acc_list  = []                                      # 存放训练次数对应的准确度的容器
    for epoch in range(1, epoches + 1, 1):
        start = perf_counter()                          # 设置一个计时起点
        for step, data in enumerate(trainloader, 0):    # 对数据集做迭代
            inputs, labels = data                       # 获得图片数据和标签数据
            inputs = inputs.cuda()
            labels = labels.cuda()
            outputs = model(inputs)                     # 获得当前模型的预测值
            
            loss = criterion(outputs, labels)           # 计算损失
            optimizer.zero_grad()                       # 重置模型梯度
            loss.backward()                             # 梯度反向传播
            optimizer.step()                            # 模型重新设置参数
            
            if step % 2000 == 0:
                step = (epoch - 1) * 12000 + step       # 计算步骤
                loss = loss.cpu().item()                # 计算损失
                acc  = 100 * test()                     # 计算准确度
                time = perf_counter() - start           # 计算时间
                start = perf_counter()                  # 重新设置计时开始点
                
                step_list.append(step)                  # 容器添加
                loss_list.append(loss)                  # 容器添加
                acc_list.append(acc)                    # 容器添加
                
                print("[Epoch:%5d Step:%5d Loss:%5.2f Acc:%5.2f%% Time:%5.2fs]"%(epoch, step, loss, acc, time)) # 日志输出
        
    print("Finished training!")                         
    return step_list, loss_list, acc_list               # 返回值

start = perf_counter()                      # 获取开始时间
Step, Loss, Acc = train(epoches)            # 获得关键训练中间数据
time = perf_counter() - start               # 计算最终训练时间
print("[Total time:%5.2fs]"%(time))

plt.figure(1)                               # 设置第 1 个画布
plt.plot(Step, Loss, 'b-')                  # 渲染第 1 个画布
plt.figure(2)                               # 设置第 2 个画布
plt.plot(Step, Acc, 'r-')                   # 渲染第 2 个画布
plt.show()                                  # 展示画布

最终，这个模型在训练 5 批次 —— 即 60,000 次训练后的正确率达到了 63%，随着训练次数的增多，准确率也会越来越高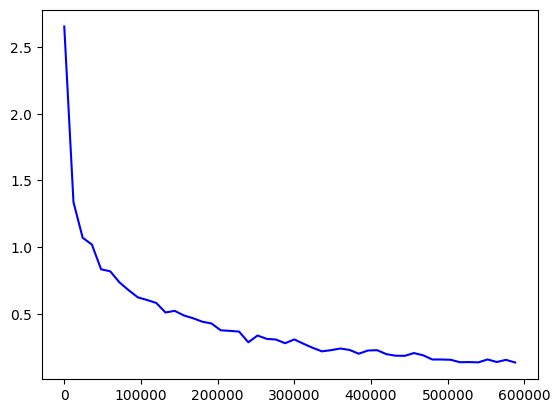

训练损失值的可视化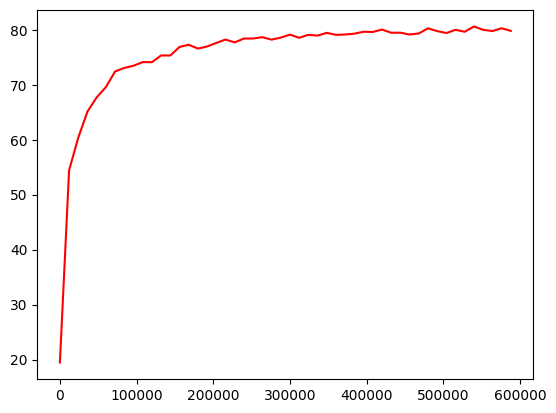

训练正确率的可视化